Investigaciones astrológicas en la oscuridad
¡Vaya! No se ha podido encontrar esa página.
Parece que no se ha encontrado nada en esta ubicación. ¿Quieres probar una búsqueda?
Coordenadas Cartesianas 3D
Para identificar la posición de un punto en el espacio utilizamos el sistema de coordenadas Cartesianas 3D. El espacio en el que nos movemos es (o parece) tridimensional. Este espacio es llamado euclídeo por los matemáticos, porque en él se cumplen las leyes geométricas de Euclides. Estos axiomas son:
-
Dados dos puntos, se puede trazar una recta entre ellos.
-
Cualquier recta se puede trazar de forma infinita en cualquier dirección.
-
Dado un punto, se puede trazar una circunferencia con cualquier radio.
-
Todos los ángulos rectos son iguales.
-
Por un punto exterior a una recta, se puede trazar una única paralela.
El espacio es tridimensional a simple vista, y en física tradicional (o Newtoniana), aunque en Física Moderna o relativista existe una cuarta dimensión que interacciona con las otras tres dimensiones espaciales.
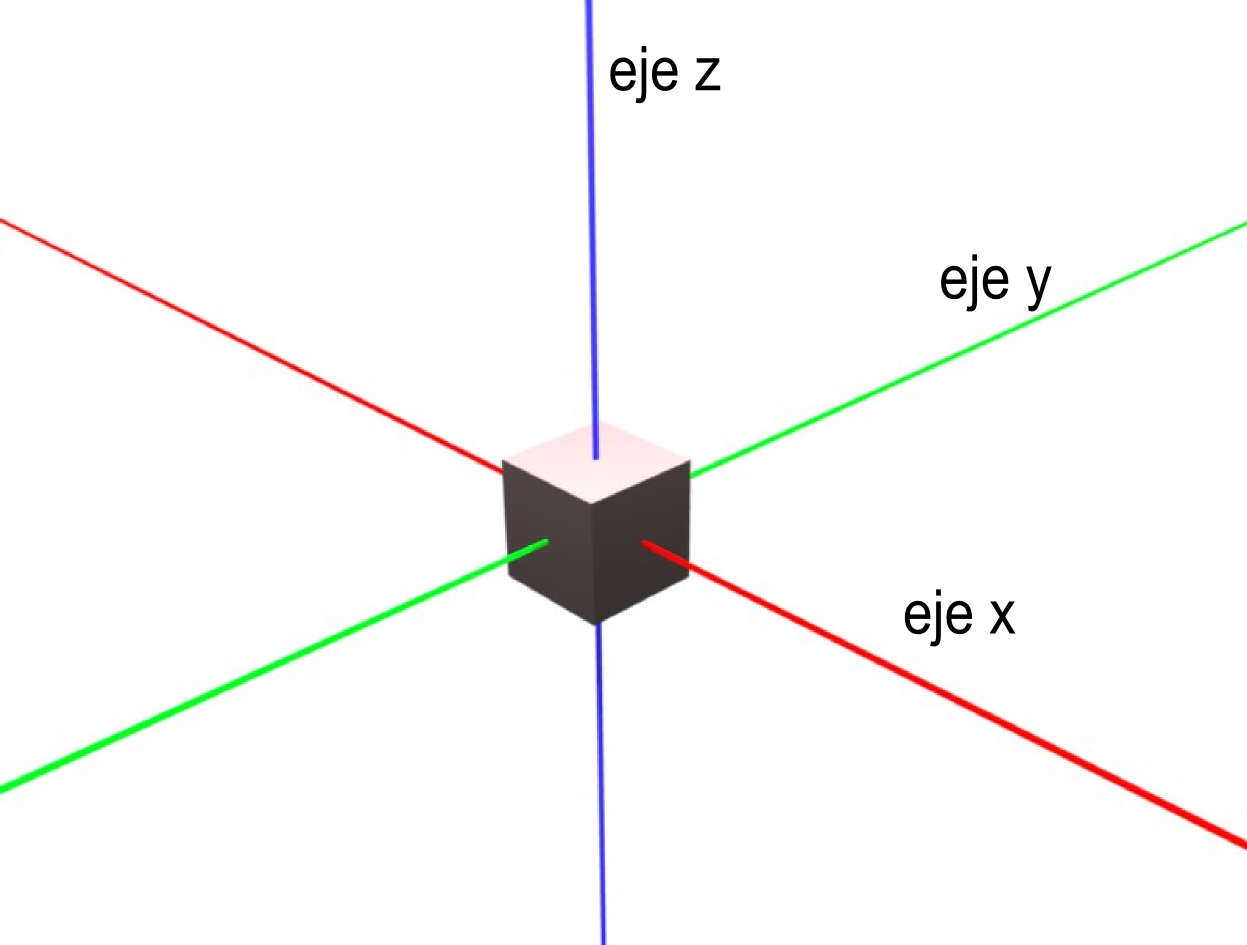 Este
sistema deriva del que ya hemos visto en dos dimensiones (2D).
Además de los ejes XY, que configuran un plano,
añadimos un tercer eje Z,
mediante el cual podemos representar un espacio tridimensional.
Las coordenadas de cualquier punto representadas mediante
este sistema tienen, por tanto, la forma A(x,y,z). En la
siguiente imagen podemos ver un punto A representado en un espacio
tridimensional. La línea D representa la distancia desde el
punto A al origen de coordenadas O.
Este
sistema deriva del que ya hemos visto en dos dimensiones (2D).
Además de los ejes XY, que configuran un plano,
añadimos un tercer eje Z,
mediante el cual podemos representar un espacio tridimensional.
Las coordenadas de cualquier punto representadas mediante
este sistema tienen, por tanto, la forma A(x,y,z). En la
siguiente imagen podemos ver un punto A representado en un espacio
tridimensional. La línea D representa la distancia desde el
punto A al origen de coordenadas O.
Cada uno de los ejes tiene asociado un vector unitario que establece la dirección y el sentido. Estos vectores se llaman i, j, k respectivamente (para x, y, z) y en la siguiente imagen aparecen en negro, partiendo desde el Origen de coordenadas, el punto en el que se cruzan los tres ejes.
 |
Con tres ejes obtenemos tres planos: XY, XZ, YZ. Si proyectamos el punto sobre cada uno de estos tres planos, veremos el punto A y sus vectores directores.
 |
 |
 |
COORDENADAS POLARES EN EL ESPACIO
Para trabajar en tres dimensiones con coordenadas polares, es necesario definir un plano fundamental sobre el que proyectar el punto A. También debemos establecer la dirección y el sentido del eje principal, sobre el que realizar las medidas. Este eje ha de pasar por el origen.
De esta forma definimos en polares la posición tridimensional de un punto:
 |
donde r es el radio vector o distancia desde el origen hasta el punto A, φ es el ángulo que hace esta recta con el plano fundamental XY y ψ es el ángulo que hace la recta OA con el eje X. Los ángulos φ y ψ deben tener definido su sentido de crecimiento. En la siguiente imagen vemos un esquema de este sistema de coordenadas polares en el espacio en tres dimensiones.
 |
A poco que observemos, notaremos que el sistema usado en astronomía para obtener coordenadas, necesariamente es el de coordenadas polares. La causa de usar este sistema estriba en el desconocimiento de la distancia r (radio vector). Las coordenadas que se obtienen se llaman coordenadas esféricas y solamente nos dan la dirección en la que está un astro. Los distintos sistemas de coordenadas que pueden idearse, basados en las polares, se diferencias en el plano fundamental usado. Así, si el plano fundamental es el Ecuador, las coordenadas serán ecuatoriales. Si el plano es el horizonte, las coordenadas serán horizontales. Si el plano es la eclíptica, las coordenadas serán eclípticas.
En el caso de las coordenadas ecuatoriales, ψ será la declinación y φ será la Ascensión Recta.
TRANSFORMACIÓN DE POLARES A CARTESIANAS
Para pasar de coordenadas polares a cartesianas es necesario definir en la figura anterior los ejes cartesianos XYZ y las proyecciones del punto A sobre ellos:
 |
Las fórmulas de transformación son estas:
|
|
EXPLICACIÓN DE ESTAS FÓRMULAS
Si no domina la trigonometría, para comprender el origen de estas transformaciones, use éste sencillo truco visual: piense siempre en la "proyección" de la distancia r sobre cada uno de los ejes, secuencialmente. Comenzamos con la primera coordenada (X):
1. Proyecte r sobre el plano XY: el resultado será el coseno del ángulo ψ, es decir "cos ψ".
2. Proyecte "cos ψ" sobre el eje X: el resultado será el coseno del ángulo φ, es decir "cos φ".
3. Así pues, ya tenemos la primera expresión X.
Las demás se consiguen de la misma manera.
 |
|
 |
 |
|
|
|
Ultimos artículos
Últimos artículos incluidos en la web, por orden inverso de aparición (los más modernos arriba):
 Observatorios remotos
Observatorios remotos

 Software
ASCOM
Software
ASCOM

 Astrofotografos aficionados
Astrofotografos aficionados

 Religión
y astronomía
Religión
y astronomía

 Astrofotografos profesionales
Astrofotografos profesionales

 Spirit:
fin de la misión
Spirit:
fin de la misión

 Eclipse Lunar 15 de Junio 2011
Eclipse Lunar 15 de Junio 2011

 Observación Junio 2011
Observación Junio 2011

 Usar Elenin con Stellarium
Usar Elenin con Stellarium

 LISA: Ondas gravitatorias
LISA: Ondas gravitatorias

 Noviembre
2011: Cometa Elenin
Noviembre
2011: Cometa Elenin

 Observación Mayo 2011
Observación Mayo 2011

 Aumenta
la actividad solar
Aumenta
la actividad solar

 50
años del vuelo de Yuri Gagarin
50
años del vuelo de Yuri Gagarin

 Magnetosfera
de Saturno
Magnetosfera
de Saturno

 Oposición
de Saturno
Oposición
de Saturno

 Ortos y Ocasos en Madrid
Ortos y Ocasos en Madrid

 IMAX
y Cassini en Saturno
IMAX
y Cassini en Saturno

 Primeras imágenes de Mercurio
Primeras imágenes de Mercurio

 Simulador
de las Fases de la Luna
Simulador
de las Fases de la Luna

 Messenger
orbita Mercurio
Messenger
orbita Mercurio

 Simulador de Ángulo Horario
Simulador de Ángulo Horario

 Observación Abril de 2011
Observación Abril de 2011

 Observación Marzo de 2011
Observación Marzo de 2011

 La
Super Luna del 19 de Marzo de 2011
La
Super Luna del 19 de Marzo de 2011

 El
cielo hoy
El
cielo hoy

 Los rovers
marcianos
Los rovers
marcianos

 Sondas
espaciales
Sondas
espaciales
El 17 de Marzo de 2011, la nave Messenger entró en órbita a Mercurio. Artículos relacionados:

 Messenger
orbita Mercurio
Messenger
orbita Mercurio

 Messenger se acerca a Mercurio
Messenger se acerca a Mercurio

Referencias prácticas
Artículos relacionados con astronomía matemática. Cómo se miden y calculan los distintos sistemas de coordenadas y sus diferencias entre ellos:
 Coordenadas cartesianas
Coordenadas cartesianas

 Coordenadas cartesianas 3D
Coordenadas cartesianas 3D

 Coordenadas polares
Coordenadas polares

 Coordenadas horizontales
Coordenadas horizontales

 Coordenadas Ecuatoriales Absolutas
Coordenadas Ecuatoriales Absolutas

 Coordenadas Ecuatoriales Horarias
Coordenadas Ecuatoriales Horarias

 Coordenadas Eclipticas
Coordenadas Eclipticas
Posición de la Estación Espacial Internacional (ISS)
Posición en tiempo real de la ISS. La ISS viaja alrededor de la Tierra en una órbita de unos 360 Km de altura. Su velocidad media es de 27.743 km/h.Créditos Heavens-Above GmbH
NASA Astronomía Foto del Día
SOHO El Sol ahora mismo
Cortesía de la sonda SOHO de la NASAFASE de la Luna al día de hoy
Cortesía del U.S Naval ObservatoryEstadisticas web

Tutoriales Blender
Blender es un programa gratuito de diseño 3D con una increible cantidad de recursos en la red. Puedes usarlo para recrear la astronomía entre otras cosas...

Escuela de Terapias alternativas
En Madrid, centro de estudio de terapias alternativas:
- Reiki
- Geometría sagrada y cristales
- Astrología arquetípica
- Anatomía del cuerpo energético...

 Home
Home



